Estruturas de Dados Intermediário/Árvores AVL

Mesma árvore após balanceamento por altura, agora uma árvore AVL

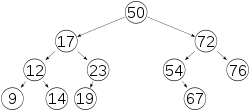
Árvore AVL (ou árvore balanceada pela altura)é uma árvore de busca binária auto-balanceada. Em tal árvore, a altura de dois nós folha difere no máximo em uma unidade. As operações de busca, inserção e eliminação de elementos possuem complexidade $O(logn)$ (no qual $n$ é o número de elementos da árvore). Inserções e eliminações podem também requerer o rebalanceamento da árvore, exigindo uma ou mais rotações.

O nome AVL vem de seus criadores Georgii Adelson Velsky e Yevgeniy Landis ,cuja primeira referência encontra-se no documento "Algoritmos para organização da informação" de 1962.

Características

Balanceamento

Uma árvore AVL é dita balanceada quando a diferença entre as alturas das sub-árvores não é maior do que um. Caso a árvore não estiver balanceada é necessário seu balanceamento através da rotação simples ou rotação dupla. O balanceamento é requerido para as operações de adição e exclusão de elementos. Para definir o balanceamento é utilizado um fator específico para nós.

O fator de balanceamento de um nó é dado pelo seu peso em relação a sua sub-árvore. Um nó com fator balanceado pode conter 1, 0, ou -1 em seu fator. Um nó com fator de balanceamento -2 ou 2 é considerado um árvore não-AVL e requer um balanceamento por rotação ou dupla-rotação.

Operações

Inserção

Inserção em uma árvore AVL deve ser dada pela inserção do nodo seguida de uma verificação na propriedade do fator de balanceamento. Caso não obedeça a essa propriedade, deve-se fazer uma rotação conveniente.

Remoção

A remoção deve ser dada por uma rotação em torno do nodo a ser removido, a fim de torná-lo folha para que então possa ser removido. Em alguns casos, após a remoção são necessárias rotações para ajustar o fator de balanceamento.

Pesquisa

O número de comparações para localizar um elemento em AVL é aproximadamente 1.44 log₂ n no pior caso.

Rotação

A operação básica em uma árvore AVL geralmente envolve os mesmos algoritmos de uma árvore de busca binária desbalanceada. A rotação na árvore AVL ocorre devido ao seu desbalanceamento, uma rotação simples ocorre quando um nó está desbalanceado e seu filho estiver no mesmo sentido da inclinação. Uma rotação-dupla ocorre quando um nó estiver desbalanceado e seu filho estiver inclinado no sentido inverso ao pai.

Rotação à esquerda

Em uma árvore binária, basta empurrar o nodo N para baixo e para a esquerda. O filho à direita de N o substitui, e o filho à esquerda do filho à direita vem a ser o novo filho à direita de N. Segue pseudocódigo:

Seja Y o filho à direita de X
Troque X por Y
Torne o filho à esquerda de Y o filho à direita de X.

Rotação à direita

Em uma árvore binária basta empurrar o nodo N para baixo e para a direita. O filho à esquerda de N o substitui, e o filho à direita do filho à esquerda vem a ser o novo filho à esquerda de N. Segue pseudocódigo:

Seja Y o filho à esquerda de X
Troque X por Y
Torne o filho à direita de Y o filho à esquerda de X.

É interessante observar que as rotações duplas nada mais são que duas rotações simples seguidas, independentes se à direita ou à esquerda.

Bibliografia

Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7.

Ligações externas