Interpolação, Ajuste de Curvas, Derivação Numérica e Integração numérica
Interpolação
[editar | editar código-fonte]Interpolação é um método para aproximar valores de seus conjuntos discretos, ou seja, a partir de determinados pontos é criado um novo conjunto de dados abrangendo os pontos previamente conhecidos. Por meio da interpolação, é possível criar uma função para esse novo conjunto de dados. A interpolação ainda pode ser dividida em alguns tipos, como: linear, polinomial e trigonométrica.
Ou seja, a Interpolação é a estimativa de um valor ou um conjunto de valores. Tendo como sua base os valores, seus contextos. Ela é basicamente uma renderização de uma linha reta entre dois ou mais pontos. Usada muitas vezes para preencher dados ausentes, como aumentar a escala de imagens. Além do mais, áreas como engenharia e ciências normalmente possuem dados pontuais extraídos de experimentos e por meio da interpolação é possível criar uma função que gere uma estimativa nestes dados. Um outro exemplo, é a utilização da interpolação para aproximar funções mais complexas para funções mais simples usando dados pontuais dessa função para a construção da função simples. Embora que, ao criar uma função mais simples, o resultado dessa função será diferente da original mas pode haver um contexto onde a utilização de métodos mais simples podem compensar o erro.[1] Basicamente a interpolação envolve a descoberta de um padrão em um conjunto de pontos de dados para estimar um valor entre dois pontos.
Até 60 anos atrás, os métodos de cálculo eram realizados manualmente e a interpolação polinomial surgiu como uma ferramenta para aproximar funções complexas que eram listadas em tabelas, em alguns valores. A interpolação polinomial é associada a Newton, porém, foi com Lagrange e Hermite que ganharam uma forma sistemática. No século XIX, Carl David Tolmé Runge e Pafnuty Lvovich Chebyshev ponderaram sobre questões de instabilidade da aproximação polinomial.[2]
Interpolação linear
[editar | editar código-fonte]É o método de interpolação que se utiliza de uma função linear p(x) (um polinômio de primeiro grau) para representar, por aproximação, uma suposta função f(x) que originalmente representaria as imagens de um intervalo descontínuo contido no domínio de f(x). A interpolação linear entre dois pontos e pode ser deduzida usando-se proporcionalidade:
daí: em um ponto (x,y). [3]
Interpolação polinomial
[editar | editar código-fonte]Diz-se interpolação polinomial quando a função interpoladora é um polinômio. A função interpoladora é a função f(x). A interpolação polinomial tem o objetivo de aproximar funções (tabeladas ou dadas por equações) por polinômios de grau até n, com o intuito de facilitar o cálculo das funções em pontos que não são dados (interpolar significa calcular pontos internos não dados).
Chama-se de interpolação ao processo de avaliar substituindo a função por uma função , tal que O é uma função real definida em , da qual conhecem-se os valores nos pontos de abcissas [4]
Os métodos de interpolação polinomial diferem, uns dos outros, quanto à técnica de determinação do polinómio interpolador. Os erros de arredondamento diferem em cada caso, pois as operações aritméticas são conduzidas de formas distintas, em cada método.
- Método de Newton
- Método de Lagrange,
- Método de Bernstein [4]
E 6.1.1. Encontre o polinômio interpolador para o conjunto de pontos {(−2, −47),
(0, −3), (1, 4), (2, 41)}.
Resolução:
Como são quatro pontos, o polinômio interpolador tera a seguinte forma: p(x) = a0 + a1X+ a2X² + a3X³
Substituindo os valores de X e Y propostos pelo problema, chegamos ao seguinte sistema linear:
a0 - 2a1+ 4a2 -8a3 = -47
a0 = -3
a0 + a1 + a2 + a3 = 4
a0 + 2a1 + 4a2 + 8a3 = 41
Ao resolver este sistema obtemos os valores:
a0 = -3
a1 = 2
a2 = 0
a3 = 5
Com estes valores, chegamos ao polinômio interpolador p(x) = -3 + 2x + 5x³
Método de Lagrange
Dado um conjunto de pontos distintos x0, x1, ..., xn n+1 e considerando para k = 0, 1, ..., n, os os seguintes polinômios l,k(x) de grau n, temos:
Logo, verificamos que:
Substituindo x por xk, observa-se que o numerador e o denominador ficam iguais \Rightarrow lk(xj) = 1. Entretanto, ao substituir x por xj, com j \ne k, verifica-se que o numerador anula, logo, lk(xj) = 0. Portanto, para valores dados de uma função , o polinômio:
Sendo de grau máximo n, satisfaz:
Logo, concluí-se, sendo Pn(x), assim definido, o polinômio de interpolação de f(x) sobre os n+1 pontos distintos x0, x1, ..., xn. [5]
Interpolação trigonométrica
[editar | editar código-fonte]A interpolação trigonométrica é processo pelo qual se obtém um polinômio trigonométrico que passa por um conjunto de pares (x,y) dados. É uma forma de interpolação adequada somente para funções periódicas.
Exemplo: Encontrar o polinômio interpolador trigonométrico de grau dois para em
de forma que e onde
Interpolação bilinear
[editar | editar código-fonte]Em matemática computacional, é uma generalização da interpolação linear de uma variável para funções de duas variáveis.
A generalização é baseada no uso da interpolação linear convencional, primeiro na direção de uma das coordenadas e, em seguida, na direção perpendicular.
A função de interpolação bilinear é:
1 2 3 4
A interpolação bilinear é usada no processamento de dados numéricos, em meteorologia e hidrodinâmica, resistência de materiais, em computação gráfica, para compensar erros no movimento da ferramenta ao longo de coordenadas em máquinas CNC, etc.
Além de interpolar um campo escalar bidimensional, ou seja, uma função de duas variáveis (coordenadas), a interpolação bilinear também é usada para interpolar campos vetoriais bidimensionais. Com esta interpolação, ambos os componentes do campo vetorial são interpolados - a projeção do vetor em pontos no eixo das coordenadas. O resultado da interpolação de duas funções escalares - componentes do vetor, gera um vetor interpolado.
Esta abordagem é usada em meteorologia para construir um mapa de vento interpolado em uma área retangular a partir dos dados medidos dos valores dos vetores de vento em pontos de controle pertencentes aos vértices do retângulo. [6]
Interpolação bilinear em computação gráfica
A necessidade de interpolação de cores no processamento digital de imagens se deve ao fato de que com um simples aumento das imagens sem processamento, ocorre uma forte pixelização da imagem.
A interpolação bilinear é usada para calcular as cores de pixels adicionais P em relação aos básicos, dados na imagem original com coordenadas de cores conhecidas Q, e o as coordenadas de cor dos pixels dentro do retângulo com as coordenadas de cor fornecidas em seus vértices, ou uma coordenada de cor no caso de imagens em tons de cinza, são calculadas em todos os pontos entre os pontos de controle, o que torna possível suavizar limites nítidos entre pixels de a imagem original. Os valores das funções {\ displaystyle f} f neste caso são calculados a partir das coordenadas das cores dos pontos de controle. Nesse caso, o lado de um quadrado formado por quatro pontos adjacentes considerados básicos costuma ser considerado um. [7]
Ajuste de Curvas
[editar | editar código-fonte]Sendo um método que observa os pontos de um conjunto, o ajuste de curva serve para criar uma curva que se ajuste a esses pontos observados. Para criar essa curva, o método pode envolver interpolação. Dentro deste método, existem também o ajuste de uma reta e o ajuste linear geral.
Ajuste de uma reta
[editar | editar código-fonte]Dentre as principais formas para resolver o problema, temos o método dos mínimos quadrados, que basicamente minimiza a soma dos quadrados residuais da regressão, melhorando assim o grau de ajuste do modelo. Utiliza esta fórmula como base: onde são os pontos exatos e são os pontos aproximados. Para o cálculo é necessário que as variantes sejam corelacionadas, caso isso não seja possível é necessário utilizar o modelo de regressão não-linear. É necessário também que o fator erro seja imprevísivel, dessa forma torna-se necessário um grande conjunto de dados para garantir um resultado mais acurado.
E 7.1.1. Sejam dados o conjunto de pontos {(0,23, −0,54), (−0,30, −0,54), (0,04, −0,57)}. Encontre a função f(x) = a1 +a2x que melhor se ajusta no sentido de mínimos quadrados aos pontos dados.
Resolução:
Utilizando as seguintes fórmulas para os coeficientes a1 e a2:
Obteremos os seguintes valores:
E substituindo na função da reta, obtemos a funçao que melhor se ajusta:
Ajuste não linear
[editar | editar código-fonte]Muitas das vezes, dados não experimentais necessitam de uma a família de funções para representá-los que não é composta por combinação linear nos parâmetros. Assim, torna-se necessário o uso de outras funções para ajustar adequadamente uma função representada na forma de tabela.
Existem casos, em que os dados experimentais sugerem que a função tabelada deve ser aproximada por uma função exponencial da forma g(x) = a(b) x , com a e b positivos. Os valores de a e b devem ser obtidos de modo que o erro seja mínimo. A função exponencial g(x) = a(b) x pode ser ajustada fazendo a seguinte transformação:
h(x) = ln(g(x)) = ln(a(b) x ) = ln(a) + xln(b)
[editar | editar código-fonte]Definindo -se assim:
a2 = ln(a), então e a2 = a
a1 = ln(b), então e a1 = b
Desta forma h(x) = ln(a) + xln(b) = a + bx é representada por uma combinação linear das funções g1(x) = x e g2(x) = 1, ou seja, h(x) = a1g1(x) + a2g2(x).
Derivação Numérica
[editar | editar código-fonte]A derivação numérica parte da interpolação, com o objetivo de calcular a derivada quando não há uma função, há apenas os pontos que pertencem a esta função. Uma das formas de resolver é através de diferenças finitas, que aproximam a derivada de uma função por meio de fórmulas que utilizam apenas um conjunto finito de pares ordenados.
Uma fórmula simples pode ser obtida através de cálculo diferencial, sendo: f'(x0) = lim (f(x0 + h) − f(x0)/h)
Dado um intervalo [a,b], e uma função f(x) derivável neste intervalo. Seja h um incremento de valor reduzido e diferente de 0, a aproximação da derivada da função f(x) em x = xk é dada por:
Um exemplo pego no site UFSJ [8] fará com que tenhamos uma facilidade na compreenção
Ex: calcular a derivada da função f(x) = ln(x) para x=1,8 com h=0,1 e 0,01 e compare com o valor real da derivada:
Valor real:
para h = 0,1
para h=0,01
Na medida em que h diminui, o valor da derivada numérica se aproxima do valor real. Porém, por menor que seja h, este método ainda apresentará um erro de arredondamento grande. Uma maneira de reduzir este erro é utilizar vários pontos.
Quanto maior o número de pontos melhor será o resultado. Porém, por praticidade, utiliza-se fórmulas de 3 a 5 pontos
Integração numérica
[editar | editar código-fonte]Esse método serve para calcular integrais definidas. Uma forma básica de fazer isso é por meio das regras de Newton-Cotes, que consiste em aproximar a integral de f por uma combinação linear de n valores de y := f(x), ou seja, essas regras são um grupo de fórmulas baseadas na avaliação do integrante em pontos igualmente espaçados.
Dentro das quadraturas das regras de Nweton-Cotes, existe a regra do ponto médio, que aproxima a função por um polinômio de grau 0; regra do trapézio, que aproxima a função por um polinômio de grau 1; e regra de Simpson, que aproxima a função por um polinômio de grau 2.
A notação é lida como “a integral de f(x) em x"e F(x) representa a função cuja derivada resulta em f(x). OU seja, F(x) é a primitiva de f(x). [9]
A notação acima demonstra uma integral indefinida, ou seja, sem definição de intervalos. Abaixo temos a mesma notação desta vez definindo intervalos de a a b
Quando a integral de f(x) pode ser expressa formalmente é possível calcular uma integral definida utilizando sua função primitiva, ou seja, a expressão formal da integral indefinida de f(x) em x
Regra do ponto médio
[editar | editar código-fonte]A regra do ponto médio é uma quadratura de Newton-Cotes de um ponto. Neste caso, temos e o polinômio interpolador é o polinômio de grau zero:
,
uma vez que . Então, temos
considerando , chegamos
Exemplo
=
Regra de Simpson
[editar | editar código-fonte]Na regra de Simpson aproximamos por um polinômio de grau , portanto precisamos de três pontos do intervalo . Utilizando, por definição,
onde .
Aproximando por e integrando temos
onde
Calculando essas integrais obtemos a regra de Simpson:
Regra dos Trapézios (simples)
[editar | editar código-fonte]A regra dos trapézios (simples), é um método numérico para obter o valor de aproximação de uma integral, define uma aproximação com certa taxa de confiabilidade, porém não é que a traz a menor margem de erro, dentre os outros métodos para calcular a integral. Dada pela fórmula: tal que, h é a diferença entre x2 e x1 (), B é x1 inserido na função f(x) e B2 é x2 inserido na função f(x).
Ex 1:
h = 4 - 1 = 3;
B = 1^2 = 1;
b = 4^2 = 16;
Com esse valores é possível jogar na fórmula, e obter o valor aproximado.
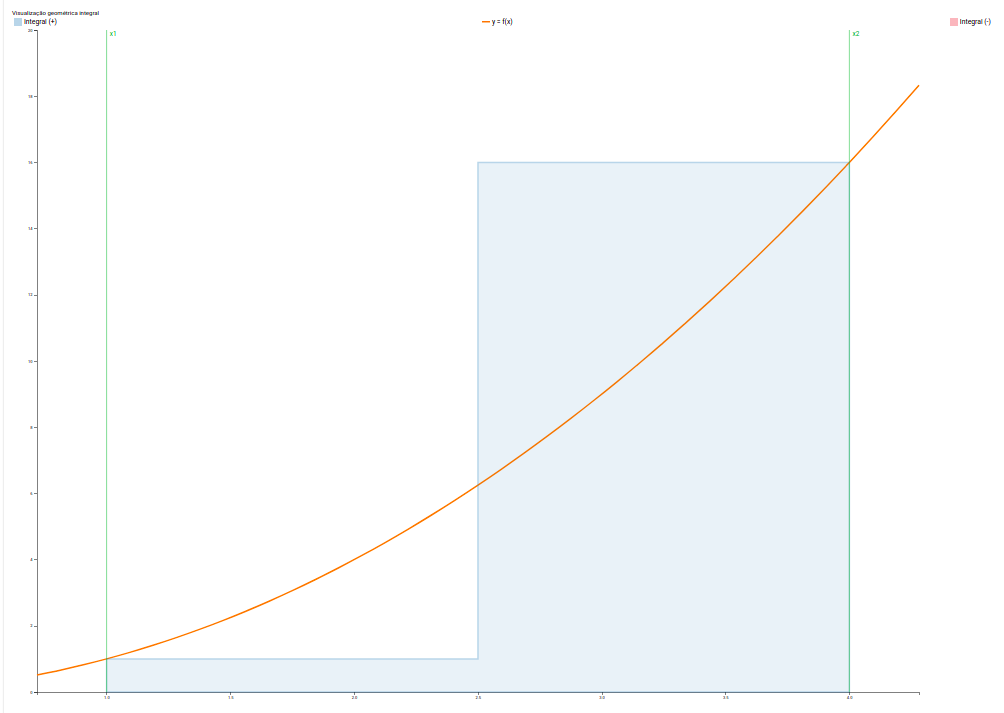
Exemplo 1 - Cálculo da integral por regra de trapézios (simples)
Ex 2:
h = 3 - 1 = 2;
B = 1^2 + 9 * 1 = 10;
b = 3^2 + 9 * 3 = 36;
Com esse valores é possível jogar na fórmula, e obter o valor aproximado.

Exemplo 2 - Cálculo da integral por regra de trapézios (simples)
- ↑ http://mc1poli.pbworks.com/f/Interpolação.pdf
- ↑ https://www.math.tecnico.ulisboa.pt/~calves/MC/cap4.html
- ↑ https://ic.ufal.br/professor/thales/icg/Aula1.2.pdf
- ↑ 4,0 4,1 http://mc1poli.pbworks.com/f/Interpola%C3%A7%C3%A3o.pdf
- ↑ https://sca.profmat-sbm.org.br/sca_v2/get_tcc3.php?cpf=84948817104&d=20180125205246&h=45185fbc723898996a18121e1b0ca3b02b905bdf
- ↑ http://weatherclasses.com/uploads/3/6/2/3/36231461/bilinear_interpolation_and_nearest_neighbor.pdf
- ↑ https://www.researchgate.net/publication/221437206_Generalised_Parallel_Bilinear_Interpolation_Architecture_for_Vision_Systems
- ↑ Nepomuceno, DERIVAÇÃO NUMÉRICA
- ↑ luzerna, Integração Numérica
- ↑ https://www.ufrgs.br/reamat/CalculoNumerico/livro-sci/in-regras_de_newton-cotes.html#x94-1610009.2.1





![{\displaystyle f(x),x\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/82c46c881cf63792ec80cd8806e144acd3371875)



![{\displaystyle [a,b]\in IR}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b21523b53c317b722d73a011e54c3d3dca4cf4a0)
![{\displaystyle z_{1},x_{2},...x_{i}...x_{n}\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/08945251f8f73a9e5170be5e05a322fc491441e1)







![{\displaystyle [0;2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e9ae5342c7722544867614790a4e3e156783beb8)







































![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)















