Problemas conceituais e filosóficos de uma nova mecânica: Bohr, Heisenberg e Einstein
Anotações para a produção de ensaio para a disciplina de Problemas conceituais e filosóficos de uma nova mecânica: Bohr, Heisenberg e Einstein do Programa de Pós Graduação em Educação Científica e Tecnológica.
Introdução
[editar | editar código-fonte]- Justificativa do interesse pelo tema(importância do tema): teletransporte e o problema da medida.
- Separar, recorte que vou realizar e com qual objetivo(intenção): Abordagem conceitual qualitativa, histórica e filosófica.
- Levar a análise.
- (considerações finais)Implicações para o ensino: Colocar em termos de perguntas, questionamentos: Essa reflexão nos levou a vários questionamentos que seriam de interesse particularmente do ensino. Uma série de perguntas que seria do interesse de pessoas/pesquisadores/professores em formação.
Justificativa
[editar | editar código-fonte]O teletransporte da informação sobre um vetor de estado quântico não é tarefa fácil mas a empreitada vale a pena pois nos ajuda a delimitar melhor conceitos como operação, medição, observação e também na compreensão sobre a falta de análogos imediatos para esses fenômenos que acontecem quando estamos trabalhando na escala quântica. As portas quânticas e a sua complexidade não serão aprofundadas aqui, vamos apenas demonstrar algumas nuances em sua aplicação. O enfoque será nas operações entre matrizes que representam as operações empíricas realizadas nos laboratórios e sobre as quais ainda não temos a menor ideia de como são realizadas. Para uma compreensão maior sobre essas operações empíricas precisaríamos de mais tempo e estudo.
Plano da obra
[editar | editar código-fonte]A seguir teremos algumas informações sobre notações corriqueiras e portas lógicas clássicas, isso tudo é para introduzir a linguagem necessária para a compreensão de como o emaranhamento e as operações com as portas lógicas nos qbits realizam/materializaram/configuram o teletransporte de informação de um vetor de estado.
Nesse processo é fundamental entender as operações e
Teletransporte quântico
[editar | editar código-fonte]O teletransporte quântico é a transferência de um estado quântico à distância. É facilitado pelo emaranhamento entre A, o doador, e B, o receptor deste estado quântico. Este processo se tornou um tópico de pesquisa fundamental para comunicação e computação quântica. Mais recentemente, os cientistas têm testado as suas aplicações na transferência de informação através de fibras ópticas. [1] O processo de teletransporte quântico é definido como o seguinte:
Alice e Bob compartilham um par EPR e cada um pegou um qubit antes de se separarem. Alice deve entregar um qubit de informações para Bob, mas ela não conhece o estado desse qubit e só pode enviar informações clássicas para Bob.
- Alice envia seus qubits através de uma porta CNOT .
- Alice então envia o primeiro qubit através de uma porta Hadamard .
- Alice mede seus qubits, obtendo um dos quatro resultados, e envia essa informação para Bob.
- Dadas as medições de Alice, Bob realiza uma das quatro operações em sua metade do par EPR e recupera o estado quântico original. [2]
O seguinte circuito quântico descreve o teletransporte:

Notações matemáticas corriqueiras
[editar | editar código-fonte]Portas lógicas
[editar | editar código-fonte]Tipos
[editar | editar código-fonte]| Tipo | Símbolo (Norma ANSI) | Símbolo (Norma IEC) | Função booleana | Tabela verdade | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AND | 
|

|
| ||||||||||||||||||||
| OR | 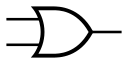
|

|
| ||||||||||||||||||||
| NOT | 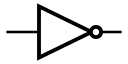
|

|
| ||||||||||||||||||||
| NAND | 
|

|
| ||||||||||||||||||||
| NOR | 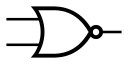
|

|
| ||||||||||||||||||||
| XOR | 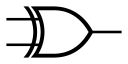
|

|
| ||||||||||||||||||||
| XNOR | 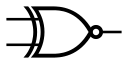
|

|
| ||||||||||||||||||||

Computação quântica
[editar | editar código-fonte]

, , , and [4]

Começando a partir de Nielsen
[editar | editar código-fonte]A base computacional
[editar | editar código-fonte]Um vetor qualquer pode ser escrito como
Operador X
[editar | editar código-fonte]No histórico do desenvolvimento da teoria a porta lógica "Não" ficou conhecida, em sua forma de matrix, como X:
Quando aplicamos X em um vetor qualquer do tipo vamos obter:
Operador Z
[editar | editar código-fonte]
Aplicando Z no vetor :
Definindo o operador Hadamard
[editar | editar código-fonte]
Conhecida como "raíz quadrada de NÃO", transforma em , e transforma em
Realizando a aplicação de H em :
A forma pode ser reescrita como:
Estados de Bell
[editar | editar código-fonte]
Embora existam muitas maneiras possíveis de criar estados de Bell emaranhados através de circuitos quânticos, a mais simples toma uma base computacional como entrada e contém uma porta Hadamard e uma porta CNOT (ver imagem). Por exemplo, o circuito quântico ilustrado recebe a entrada de dois qubits e o transforma no primeiro estado de Bell Explicitamente, o portão Hadamard transforma em uma superposição de . Isso atuará então como uma entrada de controle para a porta CNOT, que só inverte o alvo (o segundo qubit) quando o controle (o primeiro qubit) for 1. Assim, a porta CNOT transforma o segundo qubit da seguinte forma .[5][6]
Para as quatro entradas básicas de dois qubits, , o circuito gera os quatro estados de campainha ( listados acima ). Mais geralmente, o circuito transforma a entrada de acordo com a equação
As operações matriciais:[7]
Abrindo as equações:[8]
Postulado da Medição
[editar | editar código-fonte]As medidas quânticas são descritas por operadores de medida {M}. São operadores que atuam sobre o espaço de estados do sistema. Os índices se referem aos possíveis resultados da medida. Se o estado de um sistema quântico for imediatamente antes da medida, a probabilidade de um resultado ocorrer é dada por:
.
Compare o circuito de criação e o circuito do teletransporte
[editar | editar código-fonte]

Compreendendo o teletransporte[9]
[editar | editar código-fonte]Queremos enviar , dado por:
Nosso problema consiste então em:
Abrindo a expressão:
Aplicando o operador CNOT em no dois primeiros qubits para obter :
Aplicando o operador Hadamard no 1º qubit para obtermos
Ao evidenciarmos os dois primeiros qubtis de alice temos:
Agora fica evidente que dependendo da medida que Alice fizer em seus dois qubits o estado final do qubit de Bob está configurado. Essa medida de Alice vai configurar o . Ela então precisará de um canal clássico para informar Bob dos resultados de suas medidas.
- Ela mediu então ela informa Bob que ele está de posse do estado enviado.
- Ela mediu então ela informa Bob que realize uma operação de negação do seu qubit, isto é, aplique um operador X.
- Ela mediu então ela informa Bob que precisa apenas trocar o sinal da segunda parcela do qubit, isto é, aplicar um operador Z.
- Ela mediu então ela informa Bob que precisa além de negar o qubit, também é necessário trocar o sinal da segunda parcela, ou seja, é necessário aplicar o operador X e depois o operador Z.
Assim é possível realizar o teletransporte de um estado de Alice para Bob e não estamos dependendo da distância entre eles. Ainda assim é necessário um canal clássico de comunicação para informar os resultados das medidas de forma a manipular o estado do qubit que recebe a informação.
Perguntas
[editar | editar código-fonte]- Uma partícula só pode formar 1 Qbit?
- Não entendo como a não localidade aparece no emaranhamento, como pode que eu interajo com um componente e a ação se dá no outro?
Referências
- ↑ Huo, Meiru; Qin, Jiliang; Cheng, Jialin; Yan, Zhihui; Qin, Zhongzhong; Su, Xiaolong; Jia, Xiaojun; Xie, Changde; Peng, Kunchi (5 de outubro de 2018). «Deterministic quantum teleportation through fiber channels». Science Advances (em inglês) (10). ISSN 2375-2548. PMC PMC6195333
 Verifique
Verifique |pmc=(ajuda). PMID 30345350. doi:10.1126/sciadv.aas9401. Consultado em 14 de novembro de 2023 - ↑ NIELSEN, M. A.; CHUANG, I. L. '''Quantum Computation and Quantum Information: 10th Anniversary Edition'''. 10th Anniversary ed. ed. Cambridge ; New York: Cambridge University Press, 2010.
- ↑ https://en.wikipedia.org/wiki/Quantum_logic_gate
- ↑ https://en.wikipedia.org/wiki/Quantum_computing
- ↑ Traduzido da seção "Creating Bell states via quantum circuits":https://en.wikipedia.org/w/index.php?title=Bell_state&oldid=1173070664
- ↑ Consultando a página 26 de NIELSEN, M. A.; CHUANG, I. L. Quantum Computation and Quantum Information: 10th Anniversary Edition. 10th Anniversary ed. ed. Cambridge ; New York: Cambridge University Press, 2010.
- ↑ Seção da en.Wiki: Quantum_logic_gate&oldid=1183792285#The_effect_of_measurement_on_entangled_states
- ↑ Ajuda se ler p. 24 em diante.
- ↑ Retirado de https://www.ryanlarose.com/uploads/1/1/5/8/115879647/quic02.pdf


























































