Controle de fluxo refere-se à ordem em que as declarações, atribuições, instruções ou chamadas a funções são executadas ou avaliadas em um programa. Uma estrutura controle de fluxo é uma declaração cuja execução resulta em uma escolha no caminho a ser seguido para a execução de um programa. Os tipos de estrutura de controle de fluxo disponíveis podem ser diferentes em linguagens diferentes. Iremos dividir os tipos de estrutura de controle de fluxo em três tipos que serão descritos a seguir.

Estrutura sequencial : os comandos são executados de forma sequencial, seguindo a ordem em que foram declarados no código fonte. Neste tipo encontram-se instruções como jump ou goto.
Estrutura de seleção : também é chamada de expressão condicional. Neste tipo de estrutura um conjunto de ações é executado dependendo se uma determinada seleção (ou condição) é satisfeita (verdadeira) ou não (falsa).
Estrutura de repetição : este tipo de estrutura realiza a repetição de um determinado conjunto de ações dependendo se uma condição é satisfeita. Deve-se observar que, caso o código sendo executado durante as repetições nunca alterar o estado da condição, a estrutura será executada indefinidamente.

Estrutura de Seleção[editar | editar código-fonte]

As estruturas de seleção mais usadas são o "If" e o "Ifelse". Estes comandos são empregados quando deseja-se executar uma tarefa desde que uma condição seja satisfeita.

If[editar | editar código-fonte]

A sintaxe do comando if é a seguinte:

if [condição] [comando]

A sintaxe do comando "ifelse" é a seguinte:

ifelse [condição] [comando se condição for satisfeita] [comando se condição não for satisfeita]

Exemplos[editar | editar código-fonte]

Exemplo usando o comando if.

if lessp 3 4 [print [Correto!]]

Exemplo usando o comando ifelse.

ifelse equalp 10 5*2 [print [Correto!] ] [print [Errado!] ]

Programe uma calculadora em que o usuário deve entrar com a operação desejada e 2 números.

; calculadora.txt
; executa os seguintes procedimentos: adição, subtracao, divisao, multiplicação
; potencia 
; para sair digite "sair" 

to calculadora 

; Recebe entrada do usuario

print [adicao/subtracao/divisao/multiplicacao/potencia?]
make "op readlist 

print [Digite o primeiro numero]
make "var1 readWord

print [Digite o segundo numero]
make "var2 readWord

if :op = [adicao] [ print [A soma eh: ] print  :var1 + :var2] 
if :op = [subtracao] [print [A subtracao eh: ] print :var1-:var2] 
if :op = [multiplicacao] [print [A multiplicacao eh: ] print :var1*:var2] 
if :op = [divisao] [print [A divisao eh: ] print :var1 / :var2]
if :op = [potencia] [print [A subtracao eh: ] print  power :var1  :var2]

end

O comando readList ainda não havia aparecido em nossos exemplos. Ele lê uma sequência de caracteres fornecidos pelo teclado.

to sequencia

print [Qual é o próximo número da sequência: 2 4 8 16 32 64...?]
if equalp readlist [128] [print [Correto!] stop]
print [Errado, é 128.]

end

Programa que diz se um triângulo é retângulo, obtusângulo ou agudo.

to triangulo

print [Digite o valor de a: ]
make "a readWord
print [Digite o valor de b: ]
make "b readWord
print [Digite o valor de c: ]
make "c readWord

if equalp a*a b*b+c*c [print [O triangulo é retângulo.] stop]

if greaterp a*a b*b+c*c [print [O triangulo é obtusângulo.] stop]

print [O triangulo é agudo.]

end

Estrutura de Repetição[editar | editar código-fonte]

Existem duas estruturas de repetição básicas: for e while. Ambas criam um laço de repetição na qual exite uma condição para finalizar o laço. Em cada repetição (ou iteração) é executado uma determinada sequência de comandos definida pelo programador.

For[editar | editar código-fonte]

A sintaxe do laço de for é a seguinte:

for [i inicio fim] [comando]

ou

for [i inicio fim incremento] [comando]

onde i é a variação de iteração que assumirá um valor diferente a cada iteração; inicio é o valor inicial da variável de iteração; fim é o valor final da variável de iteração; e incremento é o valor do incremento que a variável de iteração sofrerá a cada iteração. O laço de for será rompido quando o valor da variável de iteração for maior do que o valor final dado pelo parâmetro fim. Caso o valor do incremento não seja fornecido, o laço de for assume que o incremento será de uma unidade.

Exemplos[editar | editar código-fonte]

? for [i 2 7 1.5] [print :i]
2
3.5
5
6.5

? for [n -1 4] [print :n]
-1
0
1
2
3
4

Imprimir 10 números aleatórios

? for [i 1 10][print random 4]

O comando "random" vai apresentar um número aleatório entre 0 e 4. Faça para outros limites.

Programa que imprime a frase "Prometo estudar!" cinquenta vezes.

for [x 1 50] [print [Prometo estudar!]]

Calcular o somatório dos números inteiros de 134 a 543

? make "soma 0
? for [n 134 543] [make "soma :soma + :n]
? print :soma
138785

Veja a figura ao lado. Ela foi criada usando o seguinte código.

to quadrado :x
repeat 4 [ fd :x lt 90 ]
end

for [n 10 250 10] [quadrado :n]

Progressão Aritmética[editar | editar código-fonte]

Podemos utilizar um loop de for para calcular a soma dos termos de uma progressão aritmética.

Progressão Aritmética (P.A.) é uma sequência numérica em que cada termo desta é igual à soma do termo anterior com uma determinada constante $r$ . O número $r$ é chamado de razão da progressão aritmética.

Podemos então a seguinte equação para determinar o n-ésimo termo da sequência, $x_{n}$ , a partir do seu antecessor $x_{n-1}$

x_{n}=x_{n-1}+r,\!\,

Exemplos[editar | editar código-fonte]

Se $r=1$ e o primeiro número da P.A. é zero:

0, 1, 2, 3, 4, 5, 6, 7, ...

Se $r=2$ e o primeiro número da P.A. é zero:

0, 2, 4, 6, 8, 10, 12, 14, ...

Se $r=3$ e o primeiro número da P.A. é um:

1, 4, 7, 10, 13, 16, 19, 22, ...

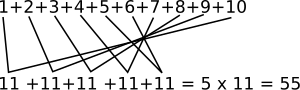
Soma dos termos de uma P.A.[editar | editar código-fonte]

Suponha que queremos somar os $N$ primeiros termos de uma P.A. com razão um e cujo primeiro termo é um. Para ilustrar, vamos inicialmente supor $N=10$ , ou seja, queremos realizar a seguinte soma:

1+2+3+4+5+6+7+8+9+10

Para realizar esta soma, podemos agrupar os termos, conforme a figura abaixo:

Note que, para qualquer $N$ sempre poderemos fazer este tipo de agrupamento: primeiro com o último, segundo com o penúltimo, etc. Desta forma a fórmula geral para calcular o somatório de $1$ a $N$ pode ser dado por

S=1+2+3+...+N=\sum _{n=1}^{N}n={\frac {N}{2}}(N+1)

Soma dos termos de uma P.A. no UCBLogo[editar | editar código-fonte]

Vamos fazer um programa simples em Logo para calcular a soma dos $N$ primeiros números de uma P.A.

Primeiramente, iremos considerar $N=10$ , para verificar o resultado obtido acima. No Logo iremos definir uma variável soma que guardará o valor da soma. Inicialmente, iremos atribuir zero a esta variável. Iremos criar um loop de for onde a variável de iteração irá iniciar no primeiro termo da sequência numérica desejada (no caso em exemplo será 1), e terminar no último termo da sequência (no caso em exemplo será 10). Em cada iteração do loop iremos somar à variável soma o valor da variável de iteração.

? make "soma 0
? for [n 1 10][make "soma :soma :n]
? print :soma
55

Podemos assim verificar que o resultado obtido está condizente.

Faça agora um exemplo para somar os números de 1 a 100.

Soma não começando do 1[editar | editar código-fonte]

Suponha agora que desejemos somar os números de 11 a 20. Esta soma não começa do 1 e portanto não podemos utilizar a fórmula acima. Mas podemos utilizar um artifício para transformar o problema atual em um problema igual ao anterior (uma soma começando do um). Para tanto iremos fazer o desenvolvimento ilustrado na figura abaixo:

S=m+(m+1)+(m+2)+...+(m+M)=m(M+1)+\sum _{n=1}^{M}n=m(M+1)+{\frac {M}{2}}(M+1)={\frac {2m+M}{2}}(M+1)

Para o caso em que o primeiro número da sequência é $m=11$ e o último número é $20$ , teremos $m+M=20$ e assim $M=9$ . Utilizando a fórmula acima

S=11+12+...+19+20={\frac {2\times 11+9}{2}}(9+1)=155

Podemos fazer o mesmo cálculo utilizando o Logo. Para tanto vamos utilizar o código abaixo.

? make "soma 0
? for [n 11 20][make "soma :soma :n]
? print :soma
155

Note que para tanto foi necessário alterar o valor inicial da variável n para 11 e o valor final da mesma para 20, desta forma, a variável n começará com o valor 11, a cada iteração do for será acrescida de um, e ao final terá o valor igual a 20.

Soma com razão diferente de 1[editar | editar código-fonte]

Os resultados até então são para somar os termos de uma P.A. com razão igual a 1. Vamos ver um exemplo de como podemos obter a soma dos termos de uma P.A. quando a razão for diferente de 1. Vamos supor que $r=2$ . Além disso, vamos começar em 1 e terminar em 11. Teremos a soma dos números ímpares:

1+3+5+7+9+11

Note que cada número pode ser expresso como um múltiplo $r$ acrescido de um, ou seja, $kr+1$ (no exemplo, $r=2$ ). Vamos escrever então:

1+3+5+7+9+11=(0\times 2)+1+(1\times 2)+1(2\times 2)+1+(3\times 2)+1+(4\times 2)+1+(5\times 2)+1

Podemos expressar esse somatório da seguinte forma

\sum _{k=0}^{5}k\times 2+1=6+\sum _{k=0}^{5}k\times 2=6+\sum _{k=1}^{5}k\times 2

De forma geral, podemos escrever a equação como

\sum _{k=0}^{\lfloor N/r\rfloor }(k\times r+1)=(\lfloor N/r\rfloor +1)+\sum _{k=1}^{\lfloor N/r\rfloor }(k\times r)

Como o $r$ é um fator comum, podemos colocá-lo em evidência no somatório, e assim teremos:

(\lfloor N/r\rfloor +1)+\sum _{k=1}^{\lfloor N/r\rfloor }(k\times r)=(\lfloor N/r\rfloor +1)+r\sum _{k=1}^{\lfloor N/r\rfloor }k

Agora encontramos um somatório igual àquele utilizado anteriormente para calcular a soma da P.A. começando em um e com razão igual a um. Vamos então utilizar o resultado anterior. Teremos assim:

(\lfloor N/r\rfloor +1)+r\sum _{k=1}^{\lfloor N/r\rfloor }k=(\lfloor N/r\rfloor +1)+r{\frac {\lfloor N/r\rfloor }{2}}(\lfloor N/r\rfloor +1)

Voltando ao exemplo do somatório (1 + 3 + 5 + 7 + 9 + 11), teremos

(5+1)+2{\frac {5}{2}}(5+1)=6+2\times 15=36

Para fazer este exemplo no Logo, iremos precisar de mais um parâmetro para o for. Este terceiro parâmetro especificará o tamanho do incremento que a variável de iteração sofrerá a cada loop. Veja o exemplo abaixo:

? make "soma 0
? for [n 1 11 2][make "soma :soma :n]
? print :soma
36

While[editar | editar código-fonte]

O loop "while" também é usado para repetições. Ele executará as instruções da lista até que a condição dada seja verdadeira.

A sintaxe do comando "while" é a seguinte:

while [condição] [comando]

Exemplos[editar | editar código-fonte]

make "x 2
while [x<5] [print [sim] make "x :x+1]

O comando acima imprime números na tela, a partir do número digitado (2). Estes números são impressos de forma crescente até o número 5.

Agora vamos sortear números aleatórios até que o usuário queira sair do programa.

to sortear
  make "p "s
  while[ :p = "s ][
     make "r random 10
     print :r 
     print [Deseja sortear outro numero (s/n)?]
     make "p readWord
     ]
end

Exemplos: Educação financeira[editar | editar código-fonte]

1. Programa para acumular dinheiro (cofrinho) No programa abaixo o usuário fornece o valor que vai guardar no cofre mensalmente e o valor mínimo que quer guardar. O programa diz quantos meses serão necessários par atingir o valor desejado.

to poupanca :x :y
   make "soma 0
   make "mes 0
   while[ :soma < :y ][
      make "soma :soma + x
      make "mes mes + 1
   ]
   print :mes
end

2. Programa poupança O usuário deve fornecer o valor que irá depositar mensalmente na poupança e o valor que ele deseja acumular. O programa irá dizer quantos meses serão necessários e qual foi o valor total acumulado na poupança. Iremos considerar que o juros da poupança é de 0,4134% ao mês.

to poupanca :x :y
   make "soma 0
   make "mes 0
   while[ :soma < :y ][
      make "soma :soma * 1.004134
      make "soma :soma + :x
      make "mes mes + 1
   ]
   print :mes
   print :soma
end

3. Outro programa Poupança Neste programa iremos supor que o usuário deseja aplicar uma certa quantia na poupança, não aplicará mais nenhum valor, e ele deseja saber quanto terá em sua poupança após um determinado número de meses.

to poupanca :soma :mes
   make "m 0
   while[ :m < :mes ][
      make "soma :soma * 1.004134
      make "m :m + 1
   ]
   print :soma
end

4. Programa financiamento Iremos calcular quantos meses serão necessários para pagar um financiamento e qual o valor total pago ao final. Será necessário fornecer o valor do financiamento, a taxa de juros aplicada e o valor da amortização desejada.

to financiamento :x :j :a
   make "mes 0
   make "pago 0
   while[:x > 0][
      make "p :j*:x + :a
      make "x :x - :a
      make "mes :mes + 1
      print :p
      make "pago :pago + :p
   ]
   print :mes
   print :pago
end

Exemplo de revisão: Sequência de Fibonacci[editar | editar código-fonte]

A sequência de Fibonacci, ou números de Fibonacci, recebe este nome em homenagem a Leonardo de Pisa, conhecido como Fibonacci. A sequência de Fibonacci é a seguinte sequência de números inteiros: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ... onde, por definição os dois primeiros números da sequência são 0 e 1, e cada número subseqüente é obtido pela soma dos dois números anteriores. A relação de recursão dos número de Fibonacci é dada então por:

F_{n}=F_{n-1}+F_{n-2},\!\,

Origem[editar | editar código-fonte]

No ocidente, a sequência de Fibonacci apareceu pela primeira vez no livro Liber Abaci (1202) de Leonardo de Pisa Albatoreul, conhecido como Fibonacci e seu irmão Warleuss Ferdynandd Albatoreul, embora ela já tivesse sido descrita por matemáticos indianos. Fibonacci considerou o crescimento de uma população idealizada (não realista biologicamente) de coelhos. Os números descrevem o número de casais na população de coelhos depois de n meses se for suposto que:

no primeiro mês nasce apenas um casal,
casais tranzão (e reproduzem-se) apenas após o segundo mês de vida,
não há problemas genéticos no cruzamento consanguíneo,
todos os meses, cada casal fértil dá a luz a um novo casal, e
os coelhos nunca morrem.

Curiosidades[editar | editar código-fonte]

Os números de Fibonacci aparecem na fórmula das diagonais de um triângulo de Pascal.
A taxa de crescimento dos números de Fibonacci, que é F(n + 1) /F(n), tende à Proporção áurea.
Os números de Fibonacci aparecem na natureza, em padrões biológicos, tal como ramificação de árvores, arranjos de folhas em um galho, o florescimento de uma alcachofra, os espirais em conchas, as curvas em ondas, etc.

Os números de Fibonacci são a soma das diagonais "sombra" (mostradas em vermelho) de triângulo de Pascal.

to fibonacci :N
   make "fib1 1
   make "fib2 1
   print fib1
   print fib2
   if :N > 2 [
      repeat :N - 2[
         make "temp :fib1
         make "fib1 :fib2
         make "fib2 sum :fib2 :temp
         print fib2
      ]
   ]
end

? fibonacci 10
1
1
2
3
5
8
13
21
34
55